The Aesthetics of Task Problems

by Jonathan Levitt and Jeremy Morse

Two new books came out in the same week of April, 1995: Secrets of Spectacular Chess (Jon Levitt and David Friedgood, Batsford, known henceforth in this article as SOS) and Chess Problems: Tasks and Records (Jeremy Morse, Faber and Faber - T&R).

Both books had a foreword by John Nunn and several positions were also shared (e.g. SOS 1.8, 5.8, 8.20 = T&R 818, 807, 642). All of this was pure coincidence. The books are quite independent of one another and cover different subjects: T&R looks systematically at task achievement in #2 problems and also at promotion and length records in problems of all types while SOS puts forward a general theory of chess aesthetics, applicable to problems, studies and the game. It seemed an interesting idea to see how well the theory of one book applied to the subject matter of the other, and this article explores the common ground - the aesthetics of task and record problems.

Readers unfamiliar with the notions of paradox (P), depth (D), geometry (G) and flow (F) or the idea of a ‘task’ should still be able to follow the examples and commentary given here.
More detailed definitions of P, D, G and F are in SOS, and the distinction between a task and a record is made clear in T&R. Before all these abbreviations drive you to despair, we will move on to some chess.

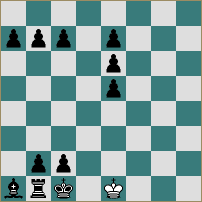
1. W.A. Shinkman (Version A. Chéron)
Mate in 8,
Deutsche Schachzeitung, 1908


The solution runs as follows:

1 b8N+ Rxb8 2 axb8N+ Kd6 3 c8N+ Ke6 4 d8N+ Bxd8
5 exd8N+ Kf6 6 g8N+ Rxg8 7 hxg8N+ Kg6 8 f8N
1-0

As you may have already guessed, the task achieved in this ingenious problem is the (maximum) effect of eight successive white promotions to a knight. It is accomplished with reasonable economy and a pure mate. Three of the four aesthetic elements stand out: the play flows across the board sweetly (F); there is always a little paradox in a single underpromotion (it is surprising that less power is more effective than more power) - and here there are eight in a row (P); the abstract pattern created by White’s play is quickly perceived by the human brain (by about move three the knight promotions are almost expected) and is classed as conceptual or ‘extended’ geometry (G). There is further graphic geometry in the row of eight white pawns in the diagram position as well as in the linear march of the black king during the solution. The element not represented is depth, since the purpose of each move is readily apparent.

Although T & R’s main focus is on task achievement, the aesthetic element is recognised in the choice of positions, with ‘good problems’ being awarded a star and ‘masterpieces’ two stars. ‘Exceptional records’ are marked with a dagger ‘regardless of their aesthetic defects’, and the Shinkman problem is included among these. Why, in the light of the analysis above, was it not given a star? The reasons are revealing.

First, although T & R’s method of judgement is not set out in any precise way, it is clear that it is primarily concerned with form, whereas SOS’s is primarily concerned with content. In justifying its award of stars, T & R occasionally refers to paradox, depth, geometry (normally as ‘pattern’) and flow, but much more often to economy, accuracy (absence of duals), harmony and diversity. Secondly, and perhaps consequentially, ‘T & R’s judgement tends to be more negative than SOS’s: T & R marks down for formal defects (such as brutal keys, duals and crowded positions), whereas SOS marks up for substantive merits. In other words, providing aesthetic content is enhanced, SOS is more ‘forgiving’ of necessary formal defects than T&R.

Hence for T & R the Shinkman problem is an exceptional task (eight white knight promotions in as many moves), but its other merits of both content and form mentioned above are outweighed by its obvious and brutal succession of checks, which make it - despite its length - one of the easiest problems in the book to solve.

This leads us back to a fascinating question already discussed in SOS, where it is said:

‘It is possible that there are forms of achievement not conveniently dealt with by our four elements. We believe our elements can be easily applied to almost all aesthetic chess positions, but it is difficult to be 'complete'. Chess art is a rich and enormous field and it is natural that there will be positions which defy attempts to categorise or explain their appeal. We considered adding a fifth element dealing with the appreciation of special forms of achievement ('special effects') but decided that it was not sufficiently useful.’

Was this decision right? After all, for Emanuel Lasker ‘achievement’ was the main aesthetic element in chess. T & R deals specifically with the sort of positions the authors of SOS had in mind when using the phrase ‘special forms of achievement’. In their lengthy debate over the issue of a possible fifth element, such problems exhibited what came to be known (informally) as ‘Factor Charlie’. Before deciding whether Factor Charlie should be labelled aesthetic, let us look at some further examples, in ascending order of aesthetic merit as we judge them.

2. C.J.Morse
Stalemate in 26
The Problemist, 1985



1 Ke2 With 2 Ke1.... and ... 26 Ke1;

the length record for stalemate with a bare white king. This problem may also be regarded as a White to play and draw study. ‘No merit except as a record.’ (T & R)

3. N.Petrovic
Mate in 2
The Problemist, 1963



1.Rgxh3

Threatens any move by either knight; all sixteen possibilities are forced by different black defences. The geometry of the two WN wheels, a maximum task, although aesthetic, is not carried by the form of the problem, with its many defects, namely: a brutal key, duals, and a crowded position.

4. V. Bartolovic &  N. Petrovic
Mate in 2
1st Hon Ment.,
BCF Tourney, 1967



1.dxc8N

Zugzwang, with a record 10 different mates after Black interferences. Formal defects (bad key, crowded position) again outweigh the limited geometry and flow of a record.

5. H.J.Burgess (version H.W.Grant & N. van Dijk)
Mate in 2
Braille Chess Magazine, 1946




1.Kb5

Zugzwang, with 9 mates after interferences. In contrast to 4), the formal merits (open position and a paradox-increasing withdrawal key) enhance the limited geometry and flow of a near-record.

6. A. F. Rudolph
Mate in 2
St Louis Globe, 1911



1.Rg4

Zugzwang; depending on Black’s reply there are 12 mates by the WQ and 6 mates by the WK. The geometry and flow of these two maximum tasks on opposite sides of the BK make a pleasing effect.

7. L.I.Loshinsky
Mate in 2
1st Hon. Mention
Tijdschrift v d Nederlandschen Schaakbond, 1930



1.Bb3

Zugzwang, with a record three Grimshaw pairs of interferences (1...f6 2 Qe4#; 1...Bf6 2 Qg4# shows the B+P Grimshaw and there are two R+B ones). Great formal merits (economy, accuracy, byplay, harmony) vastly enhance the geometry of the record. The impotence of the black pieces after the key adds an element of paradox.

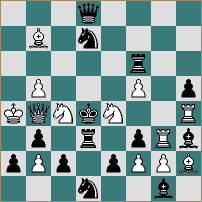
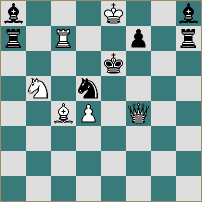
8. B.Lindgren
series selfmate in 42
1st Prize, Feenschach, 1987



In a series selfmate White plays the stipulated number of consecutive moves leading to an immediate forced mate by Black. The solution runs:

1 e8N 2 Nxf6 3 Nd5 ... 6 f8Q 7 Qxf3 8 Qg2 ... 13 f8B 14 Bxh6 15 Be3 ... 18 h8R 19 Rxh4 20 Re4 ... 25 h8Q 26 Qxb8 27 Qe5 28 b8B 29 Bxa7 30 Bc5 ... 32 a8R 33 Rxa4 34 Rb4 ... 39 a8N 40 Nab6 41 Nc4,

reaching the following position:

8a

Now 42 Qxe2+ forces Nxe2. Clear-cut presentation of a maximum task with paradox (six underpromotions), depth (8 Qg2, 34 Rb4), geometry (two Allumwandlungs), and considerable flow, and with no formal defects.

Conclusions

Looking again at the Shinkman, it is clear that some of the elements (G, F & P) are necessarily involved in the achievement of the task. The graphic geometry of the row of eight white pawns cannot be avoided! How else could you get eight consecutive white knight promotions? [It is worth pointing out there is nothing special about putting eight pawns in a row on a chessboard - it is only when this is done within the strenuous demands of a sound and economically composed problem (or study) that we have something genuinely aesthetic.] Tasks often contain inherent geometry and, similarly, record length problems are almost certain to involve flow. It can be especially impressive when the task (with its inherent aesthetics) is not only achieved, but done with such skill that further aesthetic elements are present. With this in mind, our conclusions are as follows:

1] A task has no independent aesthetic value of itself, as 2 shows.

2] A task may have inherent elements of P, D, G or F (most commonly G), but these are not necessarily strong and can easily be overcome by formal defects when there is no further PDG or F in the position as a whole. This is illustrated by 3 and 4, where the difficulty of achieving the (formidable) task has led to inelegant form. The inherent aesthetic content fails to ‘carry’ the defects of such problems.

3] Per contra, elements of P, D, G or F inherent in the task can add to the aesthetic merits of the position as a whole, whether these are substantive (as in 1 and 8) or largely formal (as in 7).

So SOS’s theory and T & R’s more subjective methods of judgement are both saved. Task achievement is not a primary aesthetic value, only a secondary and dependent one; but it can add to and enhance other aesthetic values present in a position. The distinction between beauty and achievement remains a useful one.

This article was first published in the Problemist, The official magazine of the British Chess Problem Society. Anybody interested in chess problems should join this society! You don’t have to be British...

Please write to the secretary, Christopher Jones at:
11, Severn Grange, 1 Son Hill Road, Hentsbury, Bristol, Avon BS10 7QA
Tel: 0117 950 1292
http://www.bcps.knightsfield.co.uk

If you are interested in purchasing a signed copy of ‘Secrets’ or any of my other books, click here